Изграждане на правилен многоъгълник - техническо чертане

Изграждане на вписан кръг в точното шестоъгълници-Ник. Строителство на шестоъгълника се основава на факта, че неговата страна, равна на радиуса на описаните окръжности. Следователно, достатъчно е да се изгради-точно разделяне на окръжността на шест равни части и се свързват dennye наи-точка помежду си (фиг. 60 А).

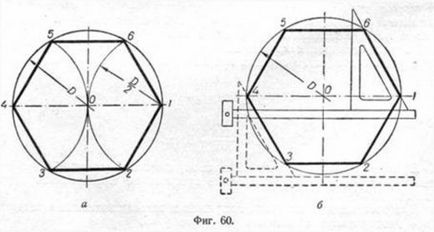
Правилен шестоъгълник може да се конструира чрез използване на Т-квадратни и квадратни 30х60 °. За да се изпълни тази конструкция приеме хоризонтален диаметър кръг на ъглополовящата на ъгъла 1 и 4 (фиг. 60, б) изграждане страна 1 -6, 4-3, 4-5 и 7-2, при което Прово дим страна 5-6 и 3-2.

Изграждане на вписан кръг на равностранен триъгълник, Ник. Върховете на този триъгълник могат да бъдат конструирани с помощта на компас и многоъгълник с ъгли 30 и 60 °, или само един от компас.

Помислете два начина на конструиране на вписан в окръжност равен-nostoronnego триъгълник.

Първият метод (фиг. 61, а) се основава на факта, че всички три ъгъла на триъгълника 7, 2, 3 съдържат 60 °, и вертикална линия през ПРОВЕРКА donnaya точка 7, е както височината и ъгъла ъглополовяща 1. Тъй като ъгълът 0-1-2 е 30 °, след това да се намери отстрани

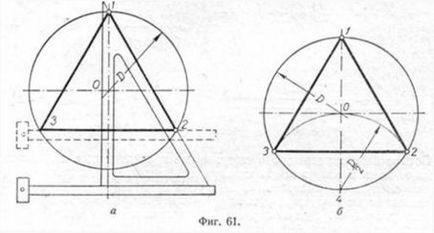
1-2 достатъчно, за да се изгради точка 1 и 0-1 страничен ъгъл от 30 ° с. За да направи това, задаване на Т-квадрат и триъгълник, както е показано на фигурата, държи линията 1-2, който ще бъде една от страните на желания триъгълник. За изграждането на страната 2-3, задаване на Т-квадрат до положението, показано с прекъснати линии, както и чрез точка 2 ПРОВЕРКА Дим линия, която ще определи третата точка.

Вторият метод се основава на факта, че ако се построи правилен шестоъгълник впише в кръг, а след това го свържете бяха автобус през един, ние получаваме един равностранен триъгълник.

За да се конструира триъгълник (фиг. 61, б) да се предвиди диаметър връх точка 1 и носи диаметрален линия 1-4. След това от точка 4 радиус равен на D / 2, описва дъга до неговото пресичане с кръг-ност в точки 3 и 2. Получените точки са другите две върховете на желания автобус триъгълник.

Конструкцията на квадрата вписан в окръжност. Тази конструкция може да се направи с квадратна и компас.

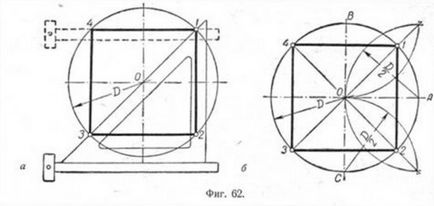
Първият метод се основава на факта, че диагоналите на квадрат повторно пресичат в центъра на окръжност кръг и наклонени към оста си под ъгъл от 45 °. Съответно, Т-квадрат и квадратен набор с ъгли от 45 °, както е показано на фиг. 62, както и маркирайте точки 1 и 3. След това чрез тези точки се извършва с помощта на Т-квадратно хоризонтално сто квадратни Rhone 4-1 и 3-2. След това използвайте Т-квадрат е по отсечка ще минем задръжте вертикална страна на площада 1-2 и 4-3.

Вторият метод се основава на факта, че върховете на квадратен разполовявам дъга, сключен между диаметъра на краищата (Фиг. 62 В). Outline краищата на две взаимно перпендикулярни диа-метър от А, В и С са в радиус на дъгата, за да опише взаимно imnogo тяхното пресичане.

Освен това, през пресечната точка на дъгите носим спомагателни mye Прекият маркирани на фигурата от плътни линии. Тяхната точка на пресичане с кръг-нето ще определи най-добре 1 и 3; 4 и 2. Получените по този начин желаните върховете на квадрат са свързани последователно един с друг.

Изграждане на вписан кръг на редовен петоъгълник.

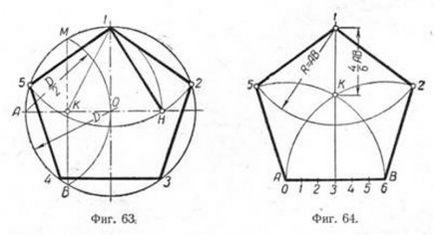
За да напишете по периферията на регулярна петоъгълник (фиг. 63), про-измъчван следните конструкции.

Планиран за 1 точка кръг и да я вземе за един от върховете на Пентагона гуми. Разделете сегмент КБ наполовина. За този радиус AB от точка А описва дъга до пресичането му с кръга в точка кортежи M и V. чрез свързването на тези точки на линията, ние получаваме точка К, който след това се комбинира с точка 1. радиус равен на сегмента А7, описва дъга от точка К до пресичането с диаметралната линия AB в точка Н. Чрез свързване точка 1 до точка Н, получаваме страна на петоъгълник. След това разтвор на компаси равна интервал 1Н, описва дъга от горния 1 до пресечната точка с окръжността, ние откриваме горната 2 и 5. Чрез същия разтвор компас резекция на върховете 2 и 5, ние получаваме останалите върховете 3 и 4. Намерено точки последователно свързване между а.

Изграждане на равностранен петоъгълник от тази страна на него.

За да се конструира редовно петоъгълник на тази страна от нея (фиг. 64) се разделят на сегмент AB на шест равни части. От точки А и В, АВ описва радиус на дъгата, преминаването на което да се отбележи След тази точка, и участък 3 на линия AB направи вертикална линия.

Следваща точка да се отложи за тази отсечка, равна на 4/6 AB.

Получаваме точка 1-връх на петоъгълник. След радиус AB от точка 1, за да се опише дъга с дъги пресичащи преди държани ЛИЗАЦИЯ на точки А и В. точките на пресичане на дъги определи петоъгълник връх 2 и 5. Намерено върховете свързани последователно една с друга.

Изграждане на вписан кръг в правилната Седмоъгълник.

Нека кръг с диаметър D; Вие трябва да го въведете в дясното Седмоъгълник (фиг. 65). Разделете вертикална диаметъра на окръжността на седем равни части. От гледна точка 7-KGS радиуси, равен на диаметъра на кръга D, описва дъга, за да се пресичат с про-доклад за хоризонтален диаметър на мястото, Е. точка F ще се нарича полигон полюс. Като VII точка за един от върховете на седмоъгълник, Прово-Дим F от поле чрез разделяне на лъчите дори вертикални диаметър, пресичане зададена с окръжност които определят върховете VI, V и IV седмоъгълник. За върховете /// - /// точки IV, V и VI за извършване на пресичане с обиколката на хоризонталните линии. Намерено връх последователност след свързване заедно. Седмоъгълник може да бъде конструиран чрез прекарване на пръст-ционни лъчи от поле F и разделяне чрез нечетен вертикален диаметър.

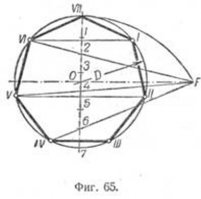
Горният метод е подходящ за изграждането на правилната полигон-ника с произволен брой страни.

периферен разделение в произволен брой равни части може да бъде про-диск, използвайки таблицата с данни. 2, което показва, коефициентът на cients, което дава възможност да се определят правилните размери изписани полигон страни.

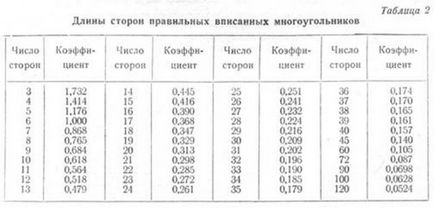
В първата колона на таблицата се посочва броят на страните, вписани правилен многоъгълник, а вторите коефициентите.

Дължината на страните на многоъгълника ще умножаване на радиуса на кръга от коефициент, съответстващ на броя на страните на многоъгълника.