Подготовка на учениците за изпита по резолюцията на център за обучение (наръчник по математика - елементите

1. Определяне на функция у = F (х) се нарича изпъкнала нагоре в интервала (а, Ь). Ако такава, че x1 2 (фиг. 2) за всеки две точки.

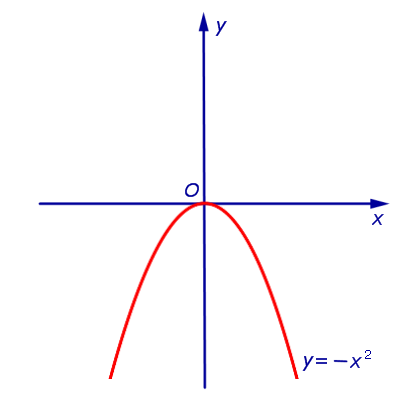
изпъкнали функции

2. Определяне на функция у = F (х) се нарича изпъкнала надолу в интервала (а, Ь). Ако такава, че x1 2 (фиг. 4) за всеки две точки.

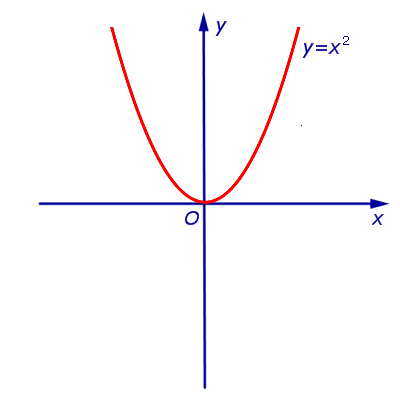
Втората производна на функцията

ОПРЕДЕЛЕНИЕ 3. Ако функция у = F (х) производно в точка x0. след това производно често се споменава като първото производно или производно на първия ред на функция у = F (х) при x0.

Да приемем, че функция у = F (х) производно във всички точки. След това във всяка точка изчисляване на производно F '(X). ние получаваме функция у = F '(х). Ако функция Y = F '(х) производно в точка x0 интервал (а, Ь), след това производно се нарича втори производно или втората производна на функция у = F (х) при x0.

За втория ред производно у = е (х) се използва следната нотация:

По същия начин, както беше направено при определянето на втората производна на F функция (X), може да се определи и производните на висок ред: трета производно, четвърто производно и т.н. (Разбира се, ако се приеме, че те съществуват).

Достатъчни условия за вдлъбната и изпъкнала надолу функция

В изпъкналост посока изследване (нагоре изпъкналост или издатина надолу) играе важна роля, втората производна на тази функция.

Резюме 1. Ако F функция (х) е в интервала (а, б) втора производно, и за всички състоянието

F функция (х) е изпъкнала надолу в интервала (а, Ь).

Претенция 2. Ако F функция (х) е в интервала (а, б) втора производно, и за всички състоянието

F функция (х) е изпъкнала нагоре в интервала (а, Ь).

Доказателства изявления 1 и 2 са извън обхвата на училище математика и не са дадени тук.

Пример 3. у функция = LN х в отговаря на интервал

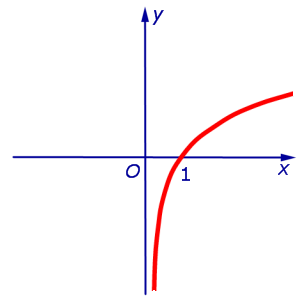
Пример 4. у функция = д х в отговаря на интервал

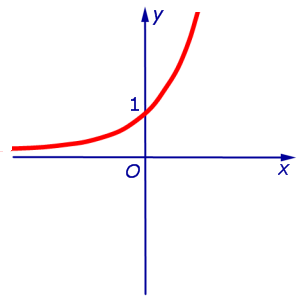
инфлексна точка

ОПРЕДЕЛЕНИЕ 4. Нека функция у = F (X), определена от интервал (а, Ь). съдържащ точка x0. Твърди се, че при преминаване през точка x0 на функцията F (х) се променя по посока на изпъкналост, ако един от интервалите

Забележка 1. Ако x0 - инфлексна точка функция у = е (х), след това графиката на функция у = е (х) при преминаване през точка x0perehodit на едната страна на допирателната в точката (x0; F (x0)) от другата страна на допирателната че е "намачкани" чрез допирателната.

Пример 5. Да разгледаме функция у = х 3. чиято графика е показано на фигура 7.

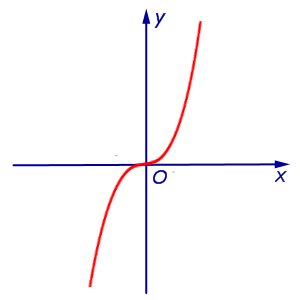
след това линия у права = 0 (х-ос Ox) е допирателна към графиката на функция у = х 3 в точката (0, 0).

Следователно у "> 0 за х> 0 и у" <0 при x <0. Таким образом, функция y = x 3 выпукла вверх при x <0 и выпукла вниз при x> 0 и точката х = 0 е инфлексна точка на графиката на у = х 3. Приложение функция у = х 3 в преминава през точката х = 0 се предава от долната половина на равнината, в горната половина, че е "прегънат" по допирателната у = 0.

Необходимите условия за съществуването на точка интонацията

Забележка 2. Условия за съществуването на точка интонацията, посочени в изявление 3, които са необходими, но не са достатъчни.

Всъщност, считаме функция у = х 4. чиято графика е показано на Фигура 8.

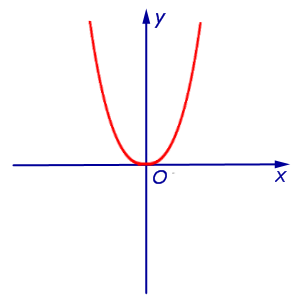
отбележи, че Y '' (0) = 0. Все пак, х = 0, точката не е точка на огъване на графиката на у = х 4. Тъй като функция у = х 4 изпъкнала. когато и двете х <0. так и при x> 0.

Достатъчни условия за съществуването на точка интонацията

Резюме 4. Нека функция у = F (X), определена от интервал (а, Ь). съдържащ точка x0. Той има първа производно във всяка точка на интервала (а, Ь) и има второ производно във всяка точка на интервала (а, Ь), с изключение може би на точка x0 на.

Ако точките на състоянието:

или състояние:

С други думи, x0 точка е инфлексна точка на графиката е (х). ако в минаваща през точка x0 втората производна промени подписват.

Пример 6. Намери интервали, когато функцията

Следователно, налице е втората производна на всички точки и става нула при точките х = 1 и х = 2. Ние използваме метода на интервали и графично на Фигура 9 диаграмата на признаци на второ производно У "(х)

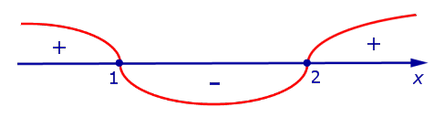
При преминаване през точката х = 1, втората производна на у "(х) се променя от знак" + "в" - "Следователно, х = 1 -. На инфлексна точка на функцията на графика.

При преминаване през точката х = 2 втората производно у "(х) променя знак от" - "до" + "Следователно, х = 2 също е инфлексната точка на графиката на ..

Ако и когато втората производна на у "(х)> 0, така че у функция (х) е изпъкнала надолу в тези интервали.

Можете също така да се запознаят с учителите, разработени център за обучение "противовъзпалително" материали за обучение, за да се подготвите за изпита по математика.

За студенти, които искат да се подготвят добре за успешно изпита по математика, физика или български език за най-висок резултат, на център за обучение "противовъзпалително" притежава