Работа и мощност на сила - основни понятия и определения
Работа на постоянна сила на прав участък
Разглеждане на материална точка М на които сила F. предположим, че точката е преместен от позиция в позиция M0 М1. си начин и (фиг. 1).
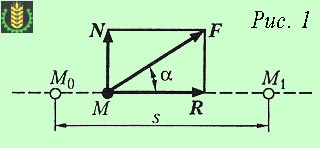
За да се установи количествена мярка за въздействие сила F на по начина, по който те. разширяване на силата на компонентите N и R. съответно насочени перпендикулярно на посоката на движение, и по него. Тъй като компонент N (перпендикулярно заместване) не може да се движи точката или устои неговото движение в посока S. Тогава действието на силата F по този начин, може да се определи произведението на компактдискове.
Тази стойност се нарича работата и е обозначен W.
Ето защо,
W = Rs = Fs защото α.
т. е. на работната сила е продукт на пътя на неговия модул и косинус на ъгъла между посоката на вектора на силата и посоката на движение на материала точка.
По този начин, работата е мярка за силата, приложена към материала в определен момент тя е преместена.
Работата е количество скаларна.
Предвид работната сила, има три специални случаи: силата е насочена по обем (α = 0˚). сила е насочена в посока обратна движение (α = 180˚). и преместване сила, перпендикулярна (α = 90˚).
Въз основа на степента на косинуса на ъгъла а. може да се заключи, че в първия случай операцията е положителен, а вторият - отрицателен, а в третия случай (защото 90˚ = 0) работна сила е нула.
Например, движение на тялото на тежестта надолу операция е положителен (вектор сила съвпада с движението), при повдигане на работата на тялото на силата на тежестта ще бъде отрицателно, докато хоризонталната движещото се тяло по отношение на работната повърхност на земята тежестта ще бъде равна на нула.
Сила, положителна работа, по-нататък движещите сили. сили, и се ангажират отрицателна работа - силите на съпротивление.
На единица работа, приет от джаул (J):
1 J = сила х х дължина = нютона m = 1 Nm.
Джоел - работна сила на един нютон на път за един метър.
Работната сила в извити участъка от пътя
На безкрайно DS на площ извит път може да бъде конвенционално разглежда като прост и сила - постоянна.
След началното работа DW сила на ДС на пътя е
DW = F DS COS (F. V).
Работата по окончателното преместване е сумата от елементарните работи:
W = ∫ F COS (F. V) DS.
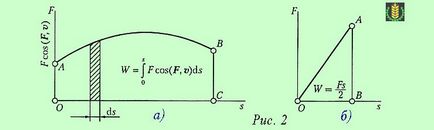
Фигура 2а показва графично представяне на зависимостта между изминатото разстояние и F COS (F. V). Площта на сенчести ивици, които безкрайно DS изместване може да се приема като правоъгълник, е елементарна работа по ДС на пътя:
DW = F COS (F. V) DS,
и работата на сила F по дългия път те се изразява графично фигури OABC площ. Limited абсциса ос, както и два ордината на крива AB. който се нарича кривата на силите.
Ако работата съвпада с посоката на преместване и нараства от нула пропорционално на пътя, операцията се изразява графично BAW триъгълник област (фиг. 2 б). който, както е известно, тя може да бъде определена от височината половината от продуктова база, т.е., половин сила работи по пътя ..:
Теорема на резултантната
Теорема: работата на получените сили на системата в определен участък от маршрута е алгебричната сума на компонентите на работната сила в един и същ участък от пътя.
Нека материална точка М се прилага система на сили (F1. F2. F3. Fn). който е резултантната на FΣ (фиг. 3).
Системата на силите прилага на материална точка, има система на конвергентни сили, следователно,
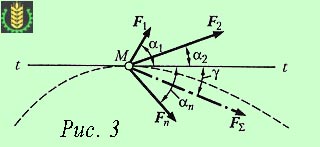
Ние проектираме вектора е равна на допирателната към пътя, последван от движещ материалната точка, а след това:
Размножава двете страни с безкрайно DS изместване и интегриране получената уравнението в някои краен обем е:
което съответства на уравнението:
Теорема на силата на тежестта
Теорема: работата на тежестта не зависи от пътя и е равна на произведението на модула за захранване на вертикалното преместване на точката му на приложение.
Нека материал минава точка М под силата на тежестта G и за определен период от време, се движи от позиция на М1 М2. си начин и (фиг. 4).
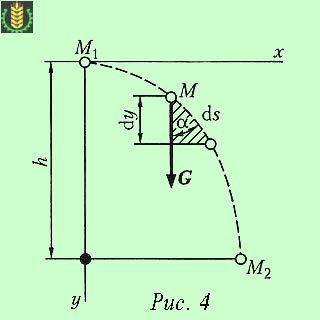
От сенчестата триъгълник, ние откриваме, че
Елементарната работата на Г сила на ДС пътят е равен на:
В общата работна сила на тежестта G е на път те
W = ∫ GDS COS α = ∫ Gdy = G ∫ Dy = Gh.
По този начин, работата на силата на тежестта е равна на произведението на силата на вертикалното преместване на точката на приложение:
Един пример за решаването на проблема с определянето на работната сила на гравитацията
Задача: Еднородна правоъгълна решетка ABCD маса М = 4080 кг има размери, показани на фиг. 5.
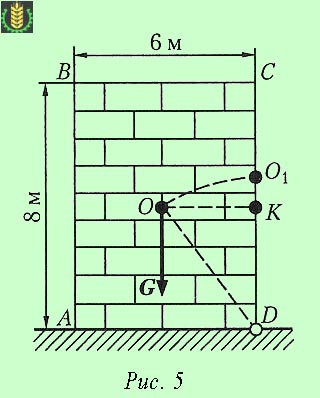
Решение.
Очевидно е, че необходимата работа е равна на съпротивлението, което се извършва от гравитацията масив, при което вертикалното движение на центъра на тежестта на масива чрез преобръщане ръб D е пътят, който определя големината на силата на гравитацията работи.
За да започне, ние определяме силата на тежестта на масива: G = мг = 4,080 х 9,81 = 40 000 N = 40 кН.
За определяне на вертикалното движение на центъра на тежестта часа еднакво правоъгълно масив (разположен в пресечната точка на диагоналите на правоъгълника), използвайки Pythagoras теорема въз основа на които:
KO1 = OD - KD = √ (KD OK 2 + 2) - KD = √ (3 февруари 2 4) - 1 = 4 м.
Въз основа на теоремата на тежестта се определи необходимата работа, необходима за накланяне на масива:
W = G х KO1 = 40 000 х 1 = 40 000 J = 40 кДж.
Работете постоянна сила, приложена към ротационното тяло
Представете диск върти около фиксирана ос при постоянна сила F (фиг. 6). Точка на приложение, което се движи заедно с диска. Ние разширяване на сила F върху три взаимно перпендикулярни компоненти: F1 - периферна сила, F2 - аксиална сила, F3 - радиална сила.
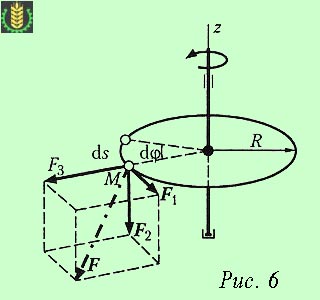
Когато завъртите селектора на безкрайно ъгъл dφ сила F ще направи начално работа, която въз основа на теоремата на полученото в работата ще бъде равна на сумата от работата на компоненти.
Очевидно е, че работата на F2 компонентите и F3 е нула, тъй като вектори на тези сили са перпендикулярни безкрайно изместване точка на DS приложение М. Следователно елементарна работата на силата F е равно на компонент му F1:
Когато диска се обърна към Ф е краен ъгъл е работата на силата F
където Ф ъгъл се изразява в радиани.
Тъй моменти компоненти F2 и F3 по отношение на оста Z са равни на нула, по теорема момент на сила F на база Varignon с отношение на Z-ос е:
В момента, на сила, приложена към диска, оста на въртене се нарича въртящ момент, както и в съответствие с ISO стандарт. означена с буквата Т.
Т = Mz (F). Следователно, W = Tφ.
Работете постоянна сила, приложена към въртящо се тяло, е продукт на въртящия момент до ъгловото изместване.
Един пример за решаване на проблема
Цел: операционната ръчка върти лебедка сила F = 200 N, перпендикулярна на радиуса на въртене.
Намери си работа, изразходвано по време Т = 25 секунди. ако една ръка г ^ = 0,4 м. и ъглова скорост ω = π / 3 рад / сек.
Решение.
На първо място, се дефинира ъглово отклонение φ лебедка дръжката за 25 секунди:
φ = ωt = (π / 3) х 25 = 26,18 рад.
На следващо място, ние използваме формулата за определяне сила операция по време на ротационното движение:
W = Tφ = Frφ = 200 х 0,4 х 26,18 ≈ 2100 ≈ 2,1 J. кДж.
Работата, извършена от сила, която може да бъде за различни периоди от време, т.е.. Д. с различна скорост. За да се характеризират как работата се извършва бързо, има концепция в механиката на властта. което обикновено се означава с буквата P.
Мощността се нарича направено за единица време работа.
Ако работата се извършва равномерно, мощността се определя по формулата

Ако посоката на сила и посоката на движение на едно и също, че тази формула може да се запише в друга форма:
P = W / т = Fs / т или P = Fv.
Мощност сила е продукт на захранващ модул от скоростта на неговата точка на приложение.
Ако операцията се извършва от сила нанася равномерно върху въртящо се тяло, силата в този случай може да се определи с формулата:
P = W / т = Tφ / т или P = Tω.
Силата на силата, приложена към равномерно въртящо се тяло е продукт на въртящ момент от ъгловата скорост.
Единицата за измерване е изходни вата (W):
W = работа / час = джаул за секунда.
Концепцията за енергийна ефективност и
Способността на тялото по време на прехода от едно състояние в друго, за да си върши работата, се нарича енергия. Енергетиката е на общата мярка на различните форми на движение на материята.
Механиката за превръщането на трансфер и енергия са различни механизми и машини, чиято цел - изпълнението на определен човек от полезни функции. В този случай, за да се прехвърлят на механизъм енергия, наречена на механичната енергия. който е коренно различна от термични, електрически, електромагнитни, ядрени и други добре известни форми на енергия. Видове на механичната енергия на тялото, които наблюдаваме, на следващата страница. но тук се определят само основните понятия и определения.
При прехвърляне или преобразуване на енергия, както и при извършване на работното място има загуби на енергия, тъй като за машини и сервиране за прехвърляне или преобразуване на различни съпротива сила енергия преодоляване (устойчивост на триене околната среда и така нататък. П.). Поради тази причина, когато прехвърлянето на част от се губи енергията и не може да се използва за извършване на полезна работа.
Ефективността на
Част от загубите на енергия по време на предаването, за да се преодолеят силите на съпротивата, отчетено чрез използването на ефективността на механизма (машина), предаване на тази енергия.
Ефективността (COP) е обозначен с η и се определя като съотношението на полезна работа (или мощност) консумира до:
Ако ефективността на механичните загуби взема предвид само, че се нарича механичната ефективност.
Очевидно е, че ефективността - винаги подходяща фракция (понякога, изразен като процент) и неговата стойност не може да бъде по-голям от един. Най-близо до единство на стойността на ефективност (100%). икономичната работа на машината.
Ако енергията или мощността, предавана следващия последователен механизъм, общата ефективност може да бъде определена като продукт на всички ефективността на механизмите: