Изследвания в 10 клас в изследването на тема - свойствата на регулярна тетраедър
Планирайте подготовка и провеждане на сесии:
I. Подготвителна фаза:- Повторението на известните свойства на триъгълна пирамида.
- Хипотези за възможните, а не преди това считат, особености на тетраедър.
- Формирането на групи за провеждане на научни изследвания в съответствие с хипотезата.
- Разпределение на задачите за всяка група (като се вземат предвид желанията).
- Разпределение на отговорностите за заданието.
- решение хипотеза.
- Консултация с учителя.
- Осъществяване работа.
- Представяне и защита на хипотезата.
- Студентски Message "Тайните на големите пирамиди".
- Встъпителни думи от учителя за видовото разнообразие на пирамидите.
- Дискусионни въпроси:
- На какво основание могат да комбинират грешна триъгълна пирамида
- Какво имаме предвид под триъгълник Ортоцентър, и това, което може да се нарече ортоцентър на тетраедър
- Има ли Ортоцентър в правоъгълен тетраедър
- Какво се нарича тетраедър isohedral какво свойства може да има
- В резултат на разглеждането на различни тетраедри, обсъждат техните свойства изяснява понятия и има някаква структура:
Информацията 1-4 доказали орално използване Slayda1.
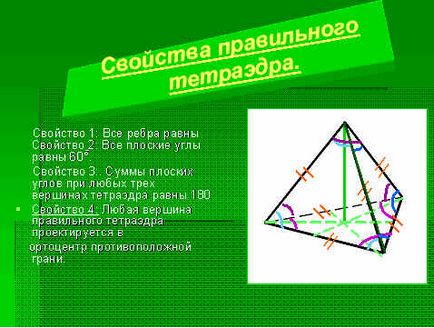
Property 1. Всички ръбове са равни.
2. Цялата собственост на ъгли на самолетни са равни на 60 °.
Property 3: Сумите са изправени ъгли и в трите върха на тетраедър е равен на 180 °.
Имоти 4. Ако тетраедър е вярна, тогава всеки връх очаква в Ортоцентър противоположната страна.
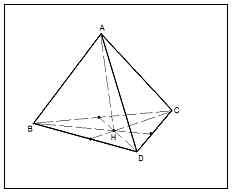
ABCD - редовно тетраедър
1) Н точка може да съвпадне с някоя от точките А, В, С Нека H? B, H? С
2) AH + (ABC) => AH + BH, AH + СН, AH + DH,
3) разглежда ABH, ВСН, ADH
AD - общ => ABH, ВСН, ADH => BH = СН = DH
AB = AC = АД г Н -. ABC е Ортоцентър
QED.- Първият урок имоти 5-9 са формулирани като хипотези, които изискват доказване.
Всяка група получава своята домашна:
Докажете, едно от свойствата.
Да изготви проучване с представянето.
II. Основният етап (през седмицата):- решение хипотеза.
- Консултация с учителя.
- Осъществяване работа.
III. Крайният етап (1-2 единици):
Представителство и защита на хипотезата, с използването на презентации.
В подготовката на материала за крайния урока, учениците стигат до заключението, че специално пресичане точка на височини, ние сме съгласни да го наричат "невероятно" точка.
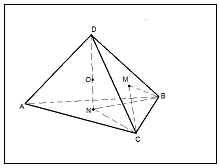
Имоти 5: центрове на определена и изписани сфери съвпадат.
DABC -proper тетраедър
O1 - центъра на сферата на окръжност
За - център на вписан областта
N - точката на допиране на вписан сферата с аспект на FAA
Да приемем, че OA = OB = OD = OC - радиусите на окръжност
Пропускане ON + (ABC)
AON = CON - правоъгълна. катет и от хипотенузата => AN = CN
Пропускане ОМ + (BCD)
COM DOM - правоъгълна. на крака и хипотенуза => CM = DM
От п. 1 CON COM => ON = OM
ON + (ABC) => ON, ОМ - радиусите на вписан кръг.
За редовна тетраедър има възможност за взаимна договореност с областта - с едно докосване на една сфера всичките си ребра. понякога Този обхват се нарича "poluvpisannoy".
Жилището е 6: сегменти, свързващи средите на срещуположните ръбове и тези ръбове са перпендикулярни сфера радиуси poluvpisannoy.
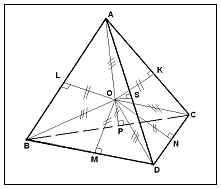
ABCD - редовно тетраедър;
AL = BL, AK = CK, AS = DS,
BP = CP, BM = DM, CN = DN.
LO = OK = OS = OM = ON = OP
Tetrahedron ABCD - надясно => AO = БО = СО = DO
Да разгледаме триъгълник АОВ, AOC, ХПК, БПК, BOC, AOD.
AO = BO => Други въпроси? - равнобедрен =>
OL - медиана, височина, ъглополовяща
AO = СО =>? AOC- равнобедрен =>
OK- медиана, височина, ъглополовяща
CO = DO =>? COD- равнобедрен =>
ON-медиана, височина, ъглополовяща на AOB => AOC = COD =
BO = DO =>? BOD- равнобедрен => БПК = BOC = AOD
OM- медиана, височина, ъглополовяща
AO = DO =>? AOD- равнобедрен =>
OS- медиана, височина, ъглополовяща
БО = СО =>? ВОС равнобедрен =>
Оперативния медиана, височина, ъглополовяща
AO = БО = СО = DO
AB = AC = AD = BC = BD = CD
3) ол, ОК, ON, OM, OS, ОП - равна по височина OL, добре, ON, ОМ, OS, радиуси ОП
сфера равнобедрен триъгълник
В редовно тетраедър да прекарате poluvpisannuyu сфера.
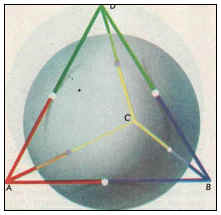
Имоти 7: Ако тетраедър е правилна, след това на всеки два противоположни края на тетраедър са взаимно перпендикулярни.
DABC - редовно тетраедър;
DABC - редовно тетраедър => ADB - равностранен
ED - височина ADB => ED + AB,
AB + CE, => AB + (EDC) => AB + CD.
По подобен начин се оказа перпендикулярността други ръбове.
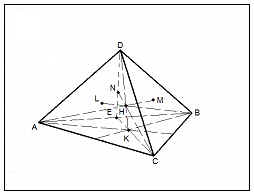
Имотът се намира на 8: Шест равнини на симетрия се пресичат в една точка. О точка пресичат четири прави линии, изготвени чрез центровете на кръгове около лицата, перпендикулярна на равнината на лицевата страна, и точка О е центъра на сферата.
ABCD - редовно тетраедър
За - центъра на сферата на окръжност;
6 равнините на симетрия се пресичат в точка О;
CG + BD. защото BCD - равностранен => GO + BD (теорема на три вертикалите GO + BD)
BG = GD, тъй AG - средната ABD
АБД (ABD) =>. BOD - равнобедрен => БО = DO
ED + AB. защото АБД -ravnostoronny => ОЕ + AD (за около три вертикалите теорема)
BE = АЕ, тъй DE - средната ABD?
ABD (ABD) => Други въпроси? - равнобедрен => BO = AO
ON + (ABC) НА + AC (за около три теорема
BF + AC, като ABC - равностранен вертикалите)
AF = FC, като BF - средната ABC?
ABC (ABC) => АОС - равнобедрен => AO = СО
БО = AO => AO = БО = СО = DO - радиус на сферата
AO = СО описано за тетраедър ABCD
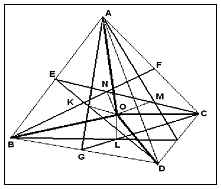
AB + (ABR) (ABR) (BCT) (ACG) (ADH) (CED) (BDF)
Точка О е в центъра на областта на окръжност,
6 равнините на симетрия се пресичат в точка О.
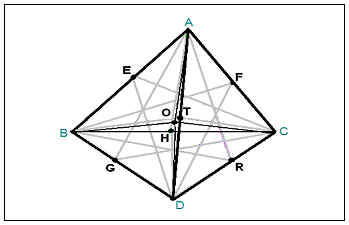
9. имот тъп ъгъл между вертикалите, преминаващи през върховете на тетраедъра да ортоцентър, е 109 ° 28 '
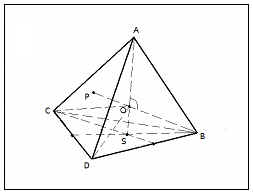
ABCD - редовно тетраедър;
О - центъра на сферата на окръжност;
ASB = 90 о OSB правоъгълна
2) (на собственост на регулярна тетраедър)
3) AO = БО - радиусите на сфера окръжност
6) AO = БО = СО = DO =>? AOD =? АОС =? AOD =? COD =? БПК =? ВОС
(Между собственост на регулярна тетраедър)
=> AOD = АОС = AOD = COD = БПК = ВОС = 109 ° 28 '
Необходимо е да се докаже.
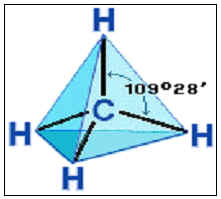
Интересен е фактът, че е този ъгъл са някои органични вещества: въглеводороди и силикати.
В резултат на това произведение на свойствата на редовни студенти Tetrahedron имаше идея да се обадите на работа "Невероятна точка в тетраедър". Имало е предложения да се вземат предвид свойствата на правоъгълна и isohedral тетраедър. По този начин, работата е отишло извън обхвата на урока.
- е точката на пресичане на трите оси на симетрия
- е точката на пресичане на шест равнини на симетрия
- е пресечната точка на височини на регулярна тетраедър
- Това е центъра на сферата вписан
- Това е в центъра на poluvpisannoy на сфера
- Това е центъра на сферата
- тетраедър е центърът на тежестта
- Той е на върха на четири равни правилните пирамиди с триъгълни бази - лицата на тетраедър.
(Учител и студенти обобщават урока. Кратко доклад за тетраедрите като структурен елемент на химичните елементи, изпълнени от един от студенти).
Свойствата на регулярна тетраедър и неговата "невероятно" точка.
Установено е, че само формата на тетраедъра като всички изброени по-горе свойства, както и на "идеална" точка може да бъде силикати и въглеводородни молекули. Или молекули могат да бъдат съставени от няколко редовен тетраедър. В момента тетраедър е известен не само като представител на древната цивилизация на математиката, но също така и като основа на структурата на материята.
Силикати - saltlike съединения, съдържащи силициев съединение с кислород. Името им идва от латинската дума "Силекс" - "кремък". Силикати молекулна база на атомно радикали, имащи форма тетраедри.
Силикати - този пясък и глина и тухли, и стъкло и цимент и емайлирани и талк и азбест, и изумрудено и топаз.
Силикати съставляват повече от 75% от кората (и с около 87% кварц) и повече от 95% от вулканични скали.
Важна характеристика е способността да силикати взаимно комбинация (полимеризация) на две или повече силиций-кислород тетраедри чрез обща кислороден атом.
Такива молекули имат същата форма като наситени въглеводороди, но те се състоят, за разлика от силикати на въглерод и водород. Общата формула на молекули
Въглеводородите включват природен газ.
Необходимо е да се помисли за свойствата на правоъгълна и isohedral тетраедър.