Какво е редовен тетраедър

Tetrahedron - това е специален случай на редовна триъгълна пирамида.

Tetrahedron - редовно полихедронов (тетраедър) с четири лица те, от своя страна, са правоъгълен триъгълник. Y 4 Tetrahedron върхове, всяка от които се събират три ребра. Общият брой на ръбове на тетраедъра 6.

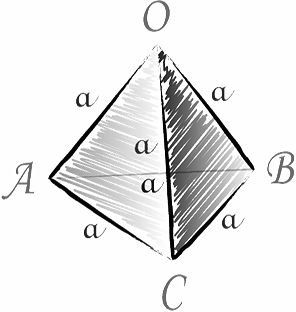
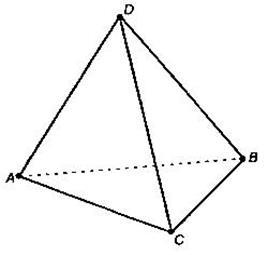
Средното тетраедър - сегмент, която свързва горната част на тетраедъра, и пресечната точка на медианите на обратната страна (медианите на равностранен триъгълник, който е противоположен на върха).

Bimediana тетраедър - сегмент, който свързва средите на ръбове, които се пресичат (свързва центъра на страните на триъгълник, което е едно от лицата на тетраедъра).

Височината на тетраедъра - сегмент, която свързва горната точка и срещуположната повърхност и перпендикуляра към това лице (т.е., височината съставен от всички изправена освен това съвпада с центъра на кръга окръжност).

Свойствата на тетраедър.

Успоредни равнини, които преминават през двойки Tetrahedron ръбове, които се пресичат и определят паралелепипед описано за тетраедър.

Самолетът, който преминава през средата на 2 Tetrahedron ръбове, които се пресичат, и го разделя на две части, идентични на обема.

Всички медиана и bimediany тетраедър се пресичат в една точка. В тази точка се разделя средно 3: 1 броене от върха. Тя разделя bimediany на две равни части.

Видове тетраедър.

Редовен тетраедър - е толкова редовен триъгълна пирамида, всяка от които е изправен, е равностранен триъгълник.

На редовното тетраедър всеки ъгъл между равнините на ръбове и всеки тристранен ъгъл във върховете имат една и съща стойност.

Tetrahedron състои от 4 лица 4 върхове и 6 ребра.

Редовен тетраедър - е един от 5 редовни polyhedra.

В допълнение към редовните тетраедър, полезни са видовете тетраедър:

- Isohedral тетраедър. то всеки аспект е триъгълник. Всички лица на тетраедър-триъгълници са равни.

- Ortotsentrichesky тетраедър. височината му всеки, падна от върха на обратната страна пресича с другите в една точка.

- Правоъгълна тетраедър. той трябваше всеки ръб, в непосредствена близост до един от върховете, ръбове перпендикулярна на друга в непосредствена близост до един и същ връх.

- Рамкова тетраедър - тетраедър, който е от следните условия:

• е сфера. който се отнася до всеки край,
• сумата от дължините на ребра, които се пресичат,
• сумата на двустенните ъгли на противоположните краища са равни,
• кръг. които са вписани в лицата по двойки докосване,
• всеки четириъгълник формира на тетраедъра сканиране - описано
• вертикалите, повдигнати по лицата на центровете на кръгове, вписани в тях, се пресичат в една точка.

- Съизмерим с тетраедър. bivysoty той същото.

- Intsentrichesky тетраедър. той сегменти, които се свързват върховете на тетраедър с центровете на кръговете, които са вписани в срещуположните повърхности се пресичат в една точка.

Формулите за определяне на елементите на тетраедър.

където H - височина на тетраедър, един - на ръба на тетраедър.

Обемът на тетраедър се изчислява съгласно класическа формулата за обема на пирамида. Необходимо е да се замести от височината и площта на регулярна тетраедър (равностранен) триъгълник.

където V - обем на тетраедъра, а - ребро на тетраедъра.

Основни формули за провеждане на редовен тетраедър:

Къде S - площта на регулярна тетраедър;

ч - височина, падна на земята;

R - радиусът на кръга вписан в тетраедър;

R - радиусът на кръга;