Комплексни числа и операциите по тях - studopediya

Комплексни числа и операциите по тях

Дори и най-простите алгебрични операции на реални числа (корен квадратен от отрицателно число, решението на квадратно уравнение с отрицателна дискриминантен) се извежда извън снимачната площадка на реални числа. Друг обобщение на понятието число води до комплексни числа. Забележителна черта на снимачната площадка на комплексни числа е, че тя е затворена по отношение на основни математически операции. С други думи, основни математически операции по сложни номера не са отстранени от снимачната площадка на комплексни числа.

Комплекс номер (в алгебрични форма) е израз

където - произволно реално число - имагинерна единица. определя от състоянието.

Броят се нарича реалната част на комплексно число е определен (от "ЯСЕН" на латински), броят се нарича имагинерна част на комплексно число и се означава с (от латинското "imaginarius").

И две комплексни числа са равни, ако и само ако те са реални и въображаеми части :. , Две комплексни числа са равни или не равни (понятието "повече" и "по-малко" не са вписани за комплексни числа).

Комплекс-конюгат на броя е броят. Очевидно, комплекс конюгат броя на броя на съвпада с номера. ,

Аритметични операции. Събиране, изваждане и умножение на комплексни числа, произведени от обикновените правила за алгебра.

Пример 1 определя комплексно число. ,

Задача 1. Нека и - един чифт комплексни числа конюгати. Покажете, че сумата им е реално число, разликата - имагинерно число и продуктът притежава валиден неотрицателно число.

Забележка. номер степен могат да бъдат представени във вид на таблица

Геометричната интерпретация на комплексно число.

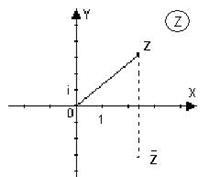
Помислете за Декартова координатна система. Се нанася по абсциса ос на комплексно число. и вертикалната ос - имагинерна част. Получаваме точка с координати. По този начин всеки комплексно число съответства на една точка на самолета. Обратно, всяка точка на самолета може да бъде свързана с комплексно число. същинската част е равна на абсцисата на точката, и имагинерна част е равна на ординатата на точката. По този начин, между комплексни числа самолета и точките на еднозначна. (По-рано, ние говорим за едно към едно съответствие между реалните числа и точките на номера на реда).

Самолетът, който посочва представляват комплексни числа се нарича комплексна равнина. За да се разграничи от реалния самолет в горния десен ъгъл на писменото писмото. кръг. абсцисната ос по такъв самолет се нарича реална ос и ординатната ос - въображаемата ос. Комплекс-конюгат - огледален образ на предварително определен брой комплекс по отношение на реалната ос. Произходът нарича нулева точка. Разстоянието на комплексното число от произхода нарича модул на този брой:

.

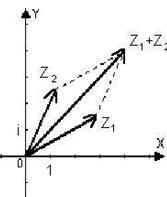
Модул на разликата на две комплексни числа - е разстоянието между съответните точки:

Всяка точка в комплексната равнина се сдружават вектора с произхода на нула цяло и в края на този етап. Очевидно е, че тази кореспонденция е едно към едно. В това тълкуване на реални и въображаеми части на комплексно число - първа и втора векторни компоненти. Сумата сега изглежда диагонал на успоредник конструирана на векторите и. разбира като разликата. Модул комплексно число представлява дължина на вектора. Геометрично очевидно е неравенството триъгълник в комплексната равнина :.

Пример 7. Определяне на мястото на точки на комплекса равнина, за който

Решение. а) Както. като се има предвид двойно неравенство може да бъде пренаписана, както :. Получихме вертикална лента.

б) От. като се има предвид двойно неравенство може да бъде пренаписана, както :. Получихме хоризонтална ивица. Задачи в) и г), за да вземе решение за себе си.

ПРИМЕР 8 посочи мястото на точки на комплекса равнина, за които а); б); в).

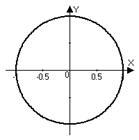
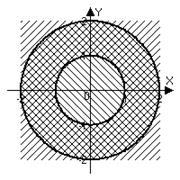
Решение. а) модул на комплексно число - това е дължината на вектора, идващи от нулевата точка до точка. т.е. разстоянието от произхода до точката. Следователно, ако е равнина на локус на точки на еднакво разстояние от произхода - е кръг (в този случай радиуса на кръга е 1). Можете да превеждате на проблема в декартови координати език:

б) Става дума за мястото на точки, които са извън кръга на радиус (центрирана в произхода).

в) точки са в пръстена, и между средите на радиус.

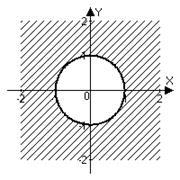
Пример 9. Дай локус на комплекса равнина, за които а); б); в).

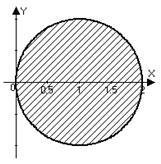
Решение. а) на модула разлика - е разстоянието между точка и точка в комплекс равнина 1. Поради това е място на точките на еднакво разстояние (на разстояние 1) от точките 1, - окръжност с радиус 1 с център в точката (1; 0). На езика на произход:

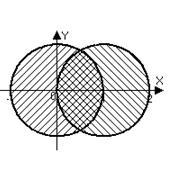
б) точки са едновременно в кръг с център в основата и по окръжност с център изместен към точката. ,

в) е на мястото на дясната полуравнина. разположена във вътрешността на кръга. ,

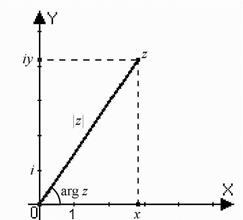
Тригонометрични форма на комплексно число. Аргументът на комплексно число се нарича ъгъл. която е вектор с положителна посока на реалната ос. Този ъгъл се определя еднозначно:

Къде - основната стойност на аргумента, че е освободен от неравенствата (т.е. комплексната равнина се извършва рязане на реалната ос отляво на произхода).

В първата колона е посочена за номера. лежи на реални или въображаеми ос, а втората колона - за останалата част от комплексни числа.

Означаваме. Тъй като. , е комплексно число може да бъде представена в тригонометрични форма:

И две комплексни числа. дефинирано в тригонометрични формата

заради неяснотата на аргумента са равни тогава и само тогава. ,

Пример 10. Намерете модулите и аргументите, както и основните ценности на аргументите на комплексни числа. Запишете всеки един от тях в тригонометрични форма.

Решение. Модули за тези номера са едни и същи:

Всяко число е аргументът, с оглед на тримесечие, което е съответната точка.

1) точката лежи в първи квадрант, а след това

Тригонометричните форма. Тя се взема предвид - честотата на синус и косинус.

2) точката се намира във втория квадрант, средства

3) точката се намира в трета квадрант, това означава,

4) точка лежи през четвъртото тримесечие, а след това,

Умножение и деление на комплексни числа в тригонометрични форма. Нека цифрите и са дефинирани в тригонометрични формата :. , Умножете ги:

Спомняйки си за формулата за косинуса и синуса на сумата от два ъгъла, получаваме

Виждаме, че в размножаването на комплексни числа, умножени техните модули и се добавят аргументи. Геометричната смисъла на тази операция, и номерата, които представляват вектори в комплексната равнина, произхождащи от нулевата точка, виждаме, че вектора, получен от вектора "разтягане" във времето и включване на корнер.

За да се получи лично формула:

Пример 11. Намерете продукта и отношението на номера

Решение. В съответствие с формула (1) могат да бъдат написани:

Ние проверяваме резултата, като се умножи тези номера в алгебрични форма:

Според формулата (2) намираме

тази операция е в алгебрични форма той може да се изписва така:

Изграждане на комплексно число на властта. От формула (1), че степенуване на комплексно число се извършва в съответствие с принципите

Пример 12. Изчисли 1); 2).

Решение. 1) Ние получихме записа на комплексно число в тригонометрични форма :. Съгласно формула (3) се намира. Същият резултат се получава по-горе Пример 4с), използвайки биномно Нютон.

2) На първо място, да си представите числата в тригонометрични форма.

Тя се намира в четвъртото тримесечие, а след това. следователно

Остава да се използва с формула (3):

Разкриване на куба на разликата, ние получаваме същия резултат (проверете!).

Във формула (3) се превръща в формула DeMoivre:

С него е лесно да се получи връзката изразяване на Синеш и уюта на множество ъгли и.

Пример 13. За да се експресира и чрез и.

Решение. Поставя формула DeMoivre. получаваме:

От ляво, за да разкрие размера на куба и събират подобни термини:

Тук имаме това. Ходихме при равенство на две комплексни числа в алгебричен вид

което е вярно, тогава и само тогава, когато са реални и въображаеми части на тези номера.

Уравнение дава реални части;

равняващи въображаеми части, ние получаваме.

Сваляне на основата на комплекс номер. Ако комплексни числа и са свързани. след това. Представлява номера в тригонометрични форма:

Предполагаме, че е налице - основната стойност на аргумент.

Нашата задача - на посочения брой (т.е. познат и), за да се определи (т.е. и двете). В съответствие с формула (3) могат да бъдат написани като уравнение

От равенството на две комплексни числа в тригонометрични форма следва:

Тук - в основата на тата степен на недвижими неотрицателно число. Следователно, за корена на та степен комплексно число ние получаваме формула

Ако приемем, че последователно. Ние се получат различни стойности:

Всички тези корени имат същите модули. т.е. съответните точки са разположени на радиуса на окръжност с център в основата. Аргументите две съседни корени на различен ъгъл. Следователно, всички стойности на корен -та степен на комплексни числа са в правилните -gon върховете вписан в окръжност с радиус.

Пример 14. Вижте всички стойности на корен-та степен на комплекс номер и ги представлява в комплекс равнина ако

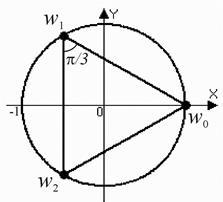
Решение. 1) На първо място, ние намираме модула и аргумента на комплексно число. , Уравнение (5) приема формата

Точките са във върховете на равностранен триъгълник вписан в окръжност с радиус, един корен - е реално число. Аргументите две съседни пиксели се различават от ъгъл. Имайте предвид, че.

2) Тук. , следователно

,

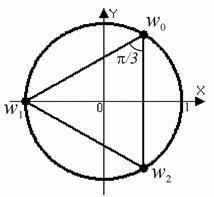
Точките са във върховете на равностранен триъгълник вписан в окръжност. корен е реално число. Имайте предвид, че. Сравнете с pr.12.2 с резултати, когато са получили. т.е. ,

3) Тук. и

,

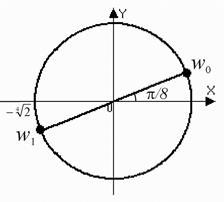
4) Ето и

. който дава две числа:

Задача 3. Извършване pr.14 работа, ако 1). 2).

Пример 15. Подреждане линейни фактори квадратен трином

Решение. 1) разглежда квадратното уравнение. Нейната дискриминантен. Така че, няма реални корени. От pr.14.4 това. Съгласно формулата за корените на квадратно уравнение. Ние получи две комплекс-конюгат корени и. В съответствие с открити корени можем да разширим квадратното трином в линейни фактори:

2) Да разгледаме квадратно уравнение. Нейната дискриминантен. няма реални корени. От pr.14.4 това. Съгласно формулата за корените на квадратно уравнение. Ние получи две комплекс-конюгат корени и. В съответствие с установените корените на квадратното трином се разлагат в линейни фактори:

Моля, имайте предвид, че квадратно уравнение с реални коефициенти има двойка сложни спрегнати корени.

Задача 4. Уверете се, че след разлагането в линейни фактори

Експоненциалното формата на комплекс номер. Формула на Ойлер (да се докаже по-късно):

Тя ви позволява да записвате комплексно число в експоненциална форма:

Тъй формула Euler и - честотата на синуса и косинуса следва:

Пример 16. Числата написани в експоненциална форма.

Лесно е да се провери валидността на:

Сравнете това съотношение на правилата за умножение и разделяне на степенуване на комплексни числа в тригонометрични форма.

Пример 17: сравнение и комплексни числа.

Решение. От pr.16 :. Има номера и модули. Отбелязването в индекса на броя на мандатите, да се откаже. представени под формата. като множител. Това означава.